本文翻译自trackpy文档，仅供学习参考

Walkthrough

分析纳米颗粒在水中的流动，跟踪轨迹并计算水滴粘度。

In [1]:

from __future__ import division, unicode_literals, print_fuction	# 为了兼容python2和python3，主要是python提前使用python的函数
import matplotlib as mpl
import matplotlib.pyplot as plt

%matplotlib inline	# ipython的魔法函数

# 可选，调整样式
mpl.rc('figure', figsize=(10, 5))
mpl.rc('image', cmap='gray')

导入python的科学计算库numpy和数据分析库pandas

导入trackpy跟踪，pims打开媒体

In [2]:

import numpy as np
import pandas as pd
from pandas import DataFrame, Series	# 为了方便

import pims
import trackpy as tp

Step 1: Read the Data

打开图片或视频

为了将数据导入Python，我们使用一个trackpy的姐妹项目PIMS(Python Image Sequence)(pims的notebook)PIMS使得通过一个一致的接口加载和处理来自多种格式的视频数据变得容易和方便。

使用 PIMS，trackpy可以读取：

一系列文件夹或压缩文件中的图片
多帧TIFF文件
一段视频(AVI、MOV等)
用于显微镜和科学视频捕捉的特殊格式：
- Cine, NorPix seq
- LSM
- Files supported by Bioformats(这个链接似乎失效了)
- ND2 using PIMS_ND2

(有些格式需要一些额外的依赖关系。有关完整列表，请参阅PIMS的README页面或文档中的安装说明。)

对于许多格式，使用pims.open就行。由于这些图像是彩色的，我们还需要设置一个管道，以便在读取图像时将其转换为灰度。

In [3]:

@pims.pipeline
def gray(image):
    return image[:, :, 1]  # Take just the green channel

frames = gray(pims.open('../sample_data/bulk_water/*.png'))

In [4]:

framses

Out [4]:

(ImageSequence,) processed through proc_func. Original repr:
    <Frames>
    Source: /Users/nkeim/projects/trackpy/trackpy-examples/sample_data/bulk_water/*.png
    Length: 300 frames
    Frame Shape: (424, 640, 4)
    Pixel Datatype: uint8

我们可以通过frames[frame_number]访问任意画面。图像被表示为一个numpy强度数组。如果你使用的是Python的Anaconda版本，这些值应该在[0,255]范围内。如果您有一个更自定义的环境，它们可能在[0,1]的范围内，在这种情况下，您将不得不试验以下最小质量参数。

In [5]:

print(frames[0])  # 第一帧

Out [5]:

[[125 125 125 ... 120 120 121]
 [125 125 125 ... 120 121 121]
 [125 125 124 ... 121 123 124]
 ...
 [125 126 125 ... 108  98  97]
 [125 125 125 ... 116 109 106]
 [125 125 125 ... 124 119 117]]

在IPython笔记本中，框架是通过显示图像直接表示的。

In [6]:

frames[0]

Out [6]:

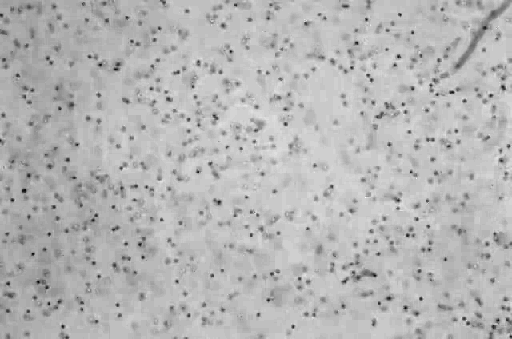
另外，要使用轴和缩放控制来绘制适当的图，可以使用matplotlib的imshow()方法。

In [7]:

plt.imshow(frames[0]);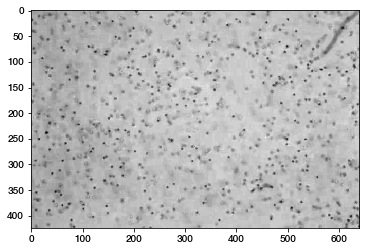

帧的行为类似于numpy数组，但有一些额外的属性。

In [8]:

frames[123].frame_no

Out [8]

In [9]:

frames[123].metadata  # 科学格式可以在这里传递实验元数据。

Out [9]

{}

Step 2: Locate Features

从第一帧开始。估计特征的大小(以像素为单位)。大小必须是一个奇数，最好是大一点，我们将在下面看到。我们估计11个像素。

In [10]:

f = tp.locate(frames[0], 11, invert=True)

算法寻找明亮的特征;由于这组图像的特征是暗的，我们设置invert=True。

locate返回一个名为DataFrame的类似电子表格的对象。它列出了:

每个特征的位置
它的外观的各种特征，我们将用它来过滤掉虚假的特征
“信号”强度和不确定度的估计都是由this paper(这是一篇粒子追踪微流变学中的静态和动态误差的文献)推导出来的

更多关于DataFrames的信息可以在pandas文档中找到。DataFrames可以很容易地导出到格式，如CSV, Excel, SQL, HDF5等。

In [11]:

f.head()  # 显示前几行数据

Out [11]

	y	x	mass	size	ecc	signal	raw_mass	ep
0	4.750000	103.668564	192.862485	2.106615	0.066390	10.808405	10714.0	0.073666
1	5.249231	585.779487	164.659302	2.962674	0.078936	4.222033	10702.0	0.075116
2	5.785986	294.792544	244.624615	2.244542	0.219217	15.874846	10686.0	0.077141
3	5.869369	338.173423	187.458282	2.046201	0.185333	13.088304	10554.0	0.099201
4	6.746377	310.584169	151.486558	3.103294	0.053342	4.475355	10403.0	0.147430

In [12]:

tp.annotate(f, frames[0]);

Out [12]

Refine parameters to elminate spurious features

(优化参数以消除虚假特征)

其中许多圈显然是错误的;它们是转瞬即逝的亮度峰值，实际上并不是粒子。删除它们通常会改善结果并加快功能查找。有很多方法可以区分真粒子和假粒子。最重要的方法是观察总亮度(“mass”)。

In [13]:

fig, ax = plt.subplots()
ax.hist(f['mass'], bins=20)

# Optionally, label the axes.
ax.set(xlabel='mass', ylabel='count');

Out [13]

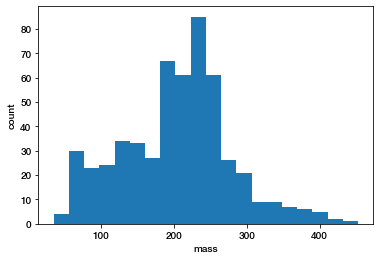
然后我们可以指定最小mass参数。

如果你的图像特别有噪声，你也会发现threshold(阈值)参数很有用。

In [14]:

f = tp.locate(frames[0], 11, invert=True, minmass=20)

In [15]:

tp.annotate(f, frames[0]);

Out [15]

有更多的控制和优化功能查找的选项。您可以在文档中查看它们，最全面的描述在API参考文档中。或者通过tp.locate?来查阅它们。

Check for subpixel accuracy

(检查亚像素精度)

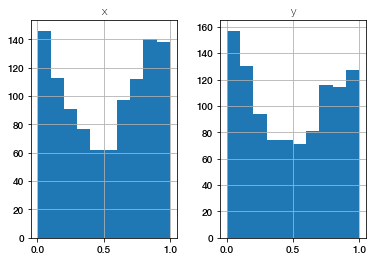
Eric Weeks在他的相关教程中指出，检查亚像素精度的一个快速方法是检查x和/或y位置的小数部分是否均匀分布。

Trackpy为此提供了一个方便的绘图函数subpx_bias:

In [16]:

tp.subpx_bias(f)

Out [16]

array([[<matplotlib.axes._subplots.AxesSubplot object at 0x1c268a1490>,
        <matplotlib.axes._subplots.AxesSubplot object at 0x1c269a54d0>]],
      dtype=object)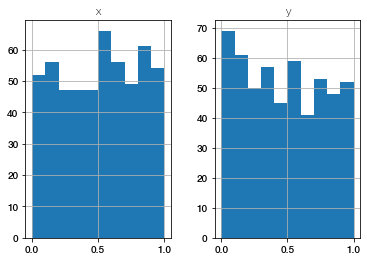

如果我们使用的像素尺寸太小，直方图经常在中间显示一个下降。

In [17]:

tp.subpx_bias(tp.locate(frames[0], 7, invert=True, minmass=20));

Out [17]

Locate features in all frames

(定位所有帧的特征)

或者，开始时，只是探索所有帧的一个子集。

selection	syntax example
all the frames	`frames[:]` or simply `frames`.
the first 10 frames	`frames[:10]`
the last 10 frames	`frames[-10:]`
a range of frames	`frames[100:200]`
every 10th frame	`frame[::10]`
a list of specific frames	`frames[[100, 107, 113]]`

我们将在这段视频的前300帧中定位特征。我们使用tp.batch调用tp.locate对每一帧分析并收集结果。

In [18]:

f = tp.batch(frames[:300], 11, minmass=20, invert=True);

Out [18]

···
Frame 299: 624 features
···

在分析每一帧时，tp.batch报告帧号和发现了多少特征。如果这个数字意外地低或高，您可能希望中断它并尝试不同的参数。

如果您的图像很小，您可能会发现打印这个数字实际上大大降低了batch速度!在这种情况下，您可以运行tp.quiet()来关闭它。

Step 3: Link features into particle trajectories

我们有粒子在每一帧中的位置。接下来，我们将逐帧跟踪粒子，给每个粒子一个编号以进行识别。

首先，我们必须指定一个最大位移，即质点在两帧间能移动的最远距离。我们应该选择最小的合理值，因为大的值会大大减慢计算时间。在这种情况下，5像素是合理的。

其次，我们考虑到粒子可能会错过几帧，然后再次看到的可能性。(可能是由于视频中的噪声，它的”mass”低于我们的截止值。)内存会跟踪消失的粒子，并在它们最后一次出现后保留它们的ID。这里我们使用3帧。

In [19]:

# tp.quiet()  # 关闭进度报告以获得最佳性能
t = tp.link(f, 5, memory=3)

Out [19]

Frame 299: 624 trajectories present.

结果是特征DataFrame f加上一个额外的列粒子，用标签标识每个特征。我们标识这个新的DataFrame为 t。

In [20]:

t.head()

Out [20]

	y	x	mass	size	ecc	signal	raw_mass	ep	particle
0	4.750000	103.668564	192.862485	2.106615	0.066390	10.808405	10714.0	0.073666	0
365	284.118980	25.313881	149.037779	2.321961	0.031799	7.008575	10770.0	0.067577	1
364	282.753601	534.788476	222.754482	1.908443	0.103416	15.874846	10415.0	0.141946	2
363	280.010398	275.185353	186.782757	2.508665	0.183181	7.261897	10438.0	0.132499	3
362	279.134153	252.780324	151.064355	2.938060	0.253812	4.306474	10359.0	0.171764	4

Filter spurious trajectories

(过滤虚假轨迹)

我们还有更多的过滤工作要做。短暂的轨迹——只能看到几帧——通常是虚假的，没有什么用处。方便的函数filter_stub只保留给定帧数的轨迹。

In [21]:

t1 = tp.filter_stubs(t, 25)
# 比较未过滤和过滤后数据中的粒子数。
print('Before:', t['particle'].nunique())
print('After:', t1['particle'].nunique())

Out [21]

Before: 13715
After: 1505

我们还可以通过粒子的外观来过滤轨迹。在这个阶段，有了轨迹连接，我们就可以通过轨迹来观察一个特征的“平均外观”，从而给出更准确的图像。

In [22]:

plt.figure()
tp.mass_size(t1.groupby('particle').mean()); # convenience function -- just plots size vs. mass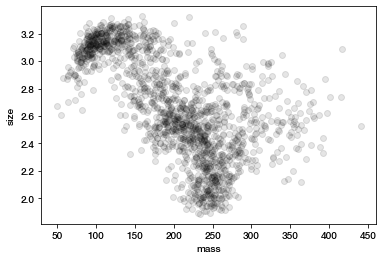

“mass”特别小的粒子，或特别大的或非圆形(偏心)的粒子，可能分别失焦或聚集。最好是通过尝试和错误进行实验，过滤出”mass”大小的空间区域，并使用tp.annotate查看结果。最后，我们需要把好的粒子从虚假的粒子中分离出来，我们如何做到这一点并不重要。

In [23]:

t2 = t1[((t1['mass'] > 50) & (t1['size'] < 2.6) &
         (t1['ecc'] < 0.3))]

In [24]:

plt.figure()
tp.annotate(t2[t2['frame'] == 0], frames[0]);

Out [24]

使用plot_traj()跟踪轨迹:

In [25]:

plt.figure()
tp.plot_traj(t2);

Out [25]

Remove overall drift

(删除整体漂移)

计算整体的漂移运动，我们将其减去，采用粒子的平均位置参考系。

In [26]:

d = tp.compute_drift(t2)

In [27]:

d.plot()
plt.show()

Out [27]

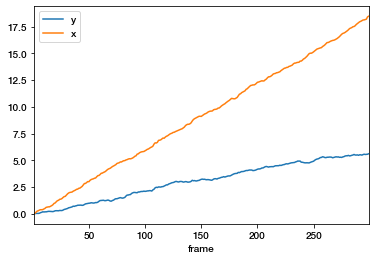
In [28]:

tm = tp.subtract_drift(t2.copy(), d)

将整个漂移运动减去，我们再次绘制轨迹。我们观察到很好的随机游动。

In [29]:

ax = tp.plot_traj(tm)
plt.show()

Step 4: Analyze trajectories

Trackpy包括几个函数，以帮助一些常见的分析粒子轨迹。(请参阅API参考的”Static Analysis”(“静态分析”)和”Motion Analysis”(“运动分析”)章节。)

在这里，我们可以证明这些数据与胶态粒子在水中经历布朗运动是一致的。

Mean Squared Displacement of Individal Probes

(单个探针的均方位移)

利用imsd函数计算每个粒子的均方位移(MSD)，并绘制MSD与滞后时间的关系图。

In [30]:

im = tp.imsd(tm, 100/285., 24)  # microns per pixel = 100/285., frames per second = 24

In [31]:

fig, ax = plt.subplots()
ax.plot(im.index, im, 'k-', alpha=0.1)  # black lines, semitransparent
ax.set(ylabel=r'$\langle \Delta r^2 \rangle$ [$\mu$m$^2$]',
       xlabel='lag time $t$')
ax.set_xscale('log')
ax.set_yscale('log')

Out [31]

因为我们只分析了300帧，所以在大延迟时间下统计数据很差。有更多的帧，我们可以研究更大的滞后时间。

Ensemble Mean Squared Displacement

(总体均方位移)

现在使用函数emsd计算所有粒子的整体均方位移(EMSD):

In [32]:

em = tp.emsd(tm, 100/285., 24) # microns per pixel = 100/285., frames per second = 24

In [33]:

fig, ax = plt.subplots()
ax.plot(em.index, em, 'o')
ax.set_xscale('log')
ax.set_yscale('log')
ax.set(ylabel=r'$\langle \Delta r^2 \rangle$ [$\mu$m$^2$]',
       xlabel='lag time $t$')
ax.set(ylim=(1e-2, 10));

Out [33]

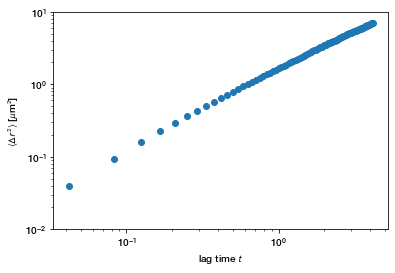
我们可以很容易地将这个集合的均方位移拟合到幂律$At^n$上，使用一个方便的函数fit_powerlaw，它在对数空间中执行线性回归。

In [34]:

plt.figure()
plt.ylabel(r'$\langle \Delta r^2 \rangle$ [$\mu$m$^2$]')
plt.xlabel('lag time $t$');
tp.utils.fit_powerlaw(em)  # 图中在对数空间执行最佳线性拟合

Out [34]

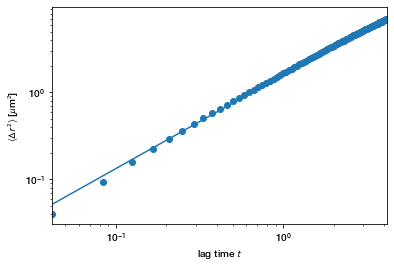
	n	A
msd	1.0787	1.595089

在水中，粘性物质，期望幂律指数$n=1$。$A=4D$，其中$D$为粒子的扩散系数。$D$通过Stokes-Einstein方程与粘度$\eta$、粒子半径$r$、温度$T$有关:
$$
D = \frac{k_BT}{6\pi\eta r}
$$
kB是玻尔兹曼常数。对于直径为1 μm的颗粒在室温水中，a≈1.66 μm2/s。上面n和A的值离我们不远了。(如果你想了解更多关于这个测量和它的不确定度，这篇文章是一个深入的讨论在高等本科水平。)